Learning-to-configure-separators

Learning to Configure Separators in Branch-and-Cut

Sirui Li*¹, Wenbin Ouyang* ¹, Max B. Paulus², Cathy Wu¹

¹MIT ²ETH Zürich

NeurIPS 2023

**Figure 1: The Separator Configuration Task.**

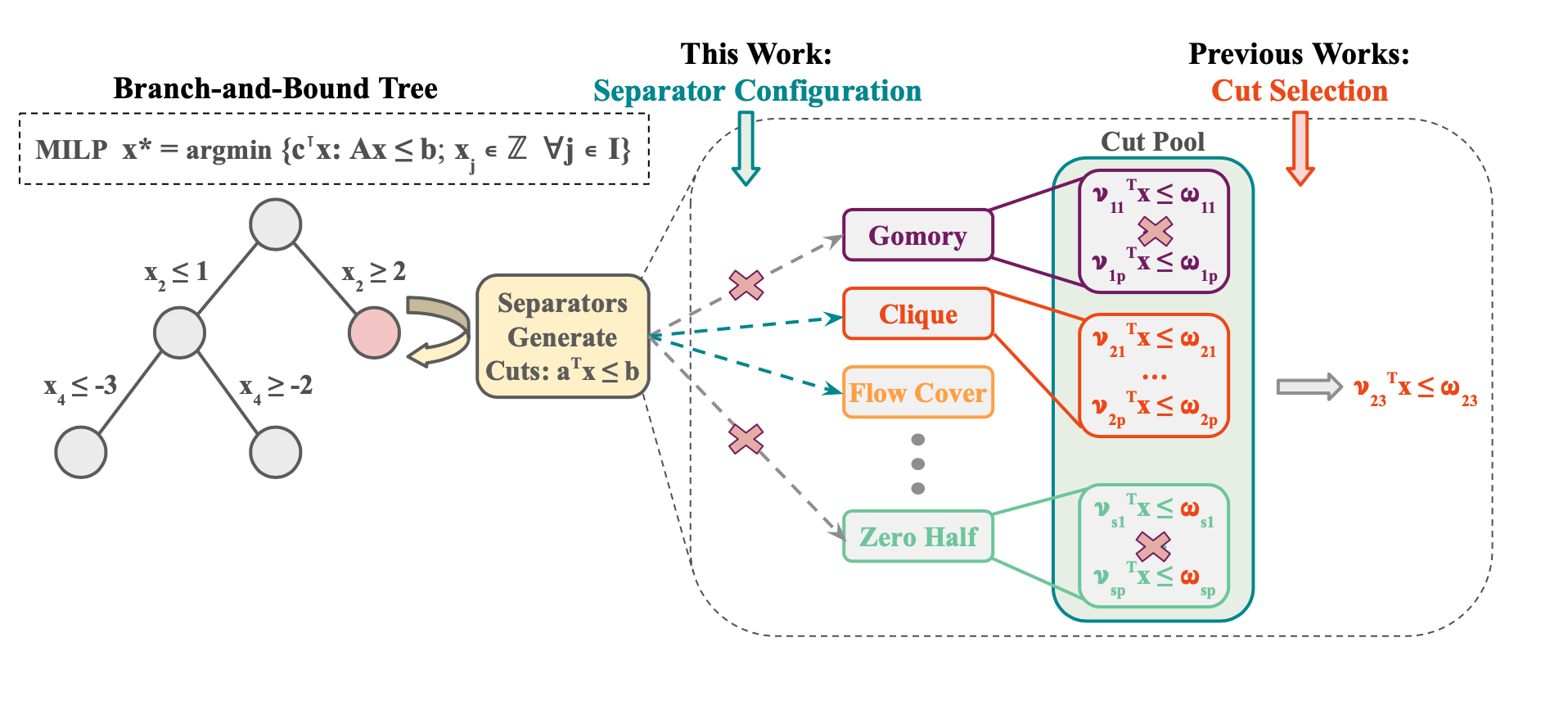
Cutting planes are crucial in solving mixed integer linear programs (MILP) as they facilitate bound improvements on the optimal solution. Modern MILP solvers rely on a variety of separators to generate a diverse set of cutting planes by invoking the separators frequently during the solving process. This work identifies that MILP solvers can be drastically accelerated by appropriately selecting separators to activate. As the combinatorial separator selection space imposes challenges for machine learning, we learn to separate by proposing a novel data-driven strategy to restrict the selection space and a learning-guided algorithm on the restricted space. Our method predicts instance-aware separator configurations which can dynamically adapt during the solve, effectively accelerating the open source MILP solver SCIP by improving the relative solve time up to 72% and 37% on synthetic and real-world MILP benchmarks. Our work complements recent work on learning to select cutting planes and highlights the importance of separator management.

Citation

    @inproceedings{li2023learning,
        title={Learning to Configure Separators in Branch-and-Bound},
        author={Sirui Li and Wenbin Ouyang and Max B. Paulus and Cathy Wu},
        booktitle={Thirty-Seventh Conference on Neural Information Processing Systems},
        year={2023},
    }

Algorithm Pipeline: L2Sep

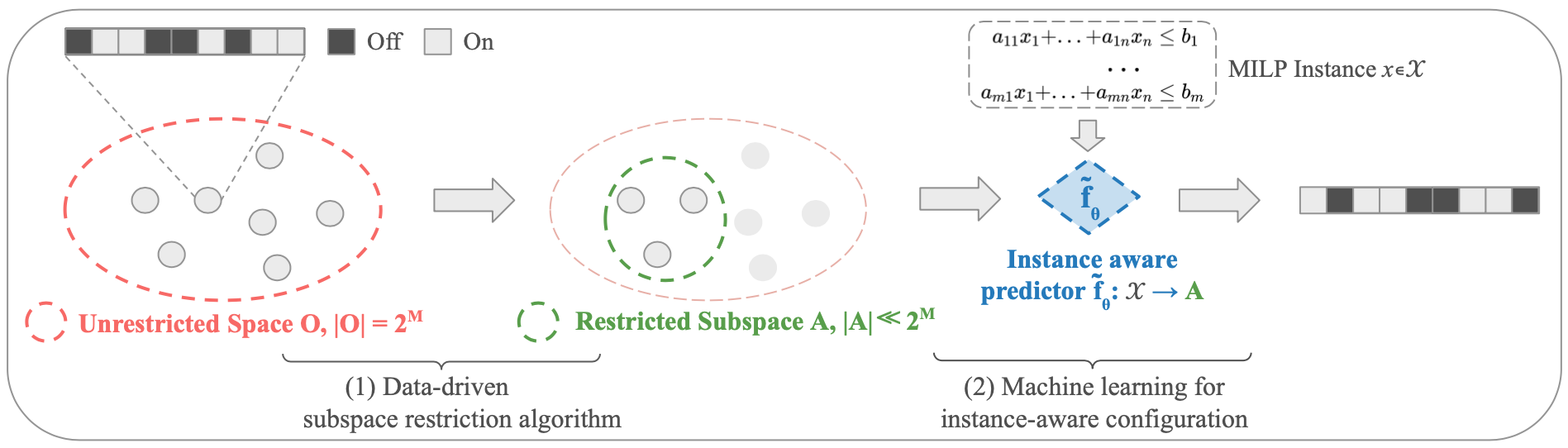
**Figure 2: The proposed learning method L2Sep.**

(1) Data-driven algorithm to find a restricted separator configuration subspace A: We select A from the full configuration space by choosing configurations that are effective but without being redundant. We devise a greedy algorithm augmented by a filtering strategy to balance training performance v.s. generalization.
** Note that Each element of the subset A is a combination of separators (e.g., Gomory, Clique) to activate; we call this a configuration and it can be thought of as a binary vector of length the number of separators (17 for SCIP).

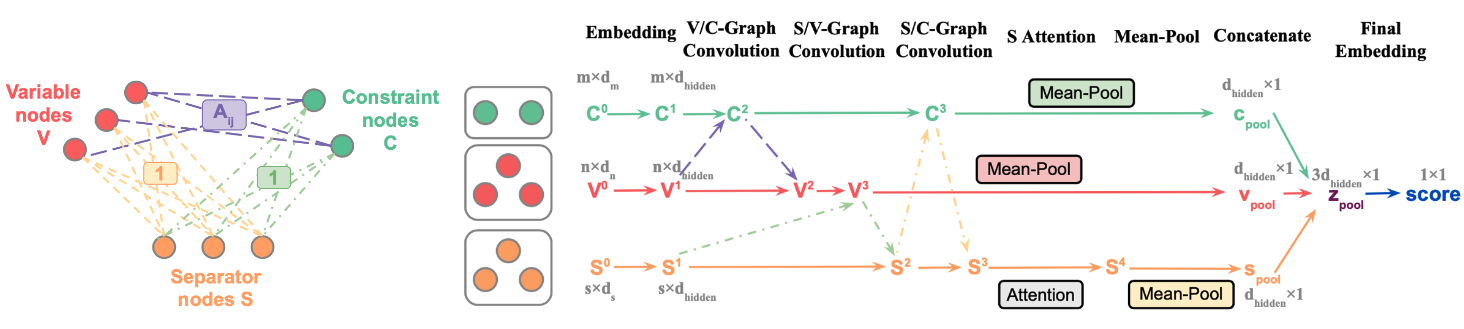
(2) Learning to configure separators within A: We perform separator configurations in k different separation rounds, while holding the configuration fixed between rounds. We apply a forward training algorithm and learn to configure at each round with the Neural UCB algorithm. We use a Graph Neural Network (GNN) to estimate the relative time improvement (reward) of applying a configuration s (arm) within A to the MILP instance x (context) from the default separator configuration of the MILP solver.

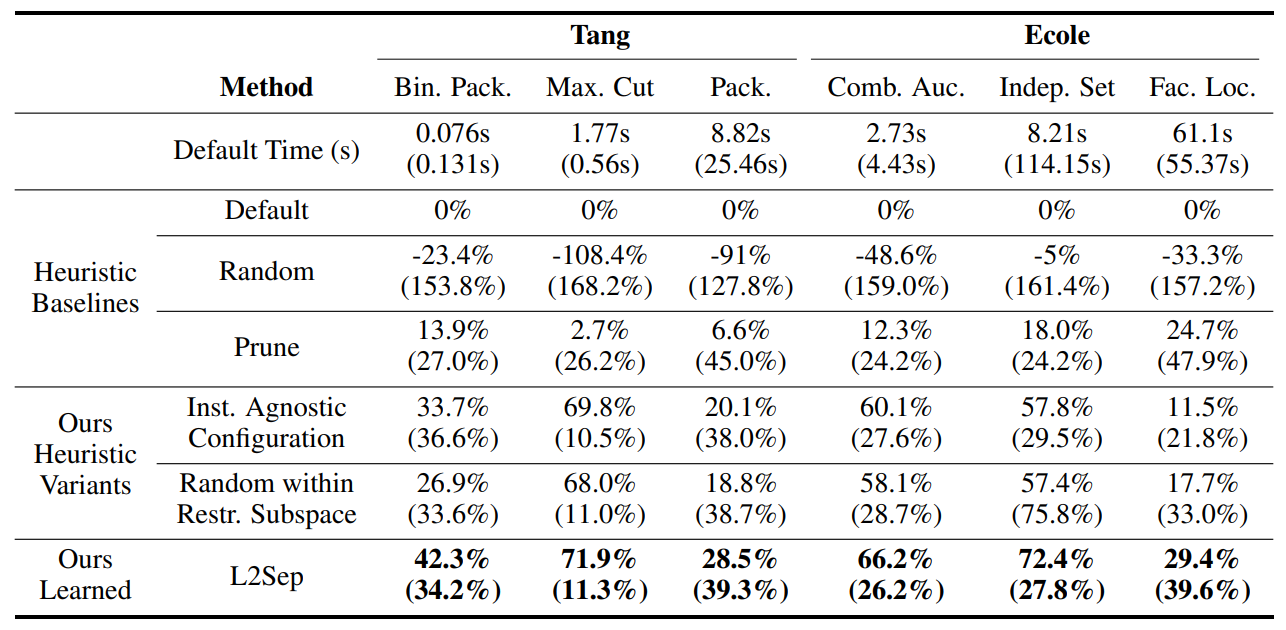
Experimental Results

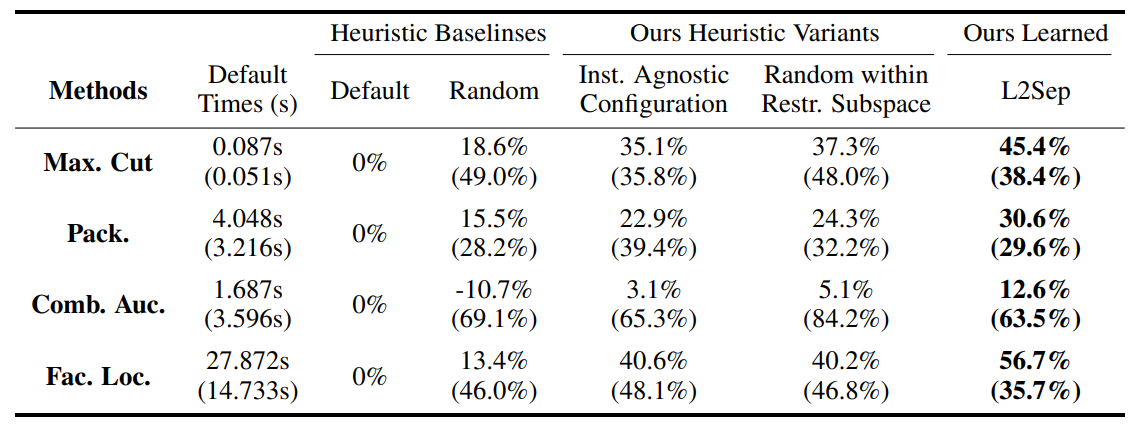
L2Sep achieves 30%-to-70% speedup on a variety of MILP datasets

**Table 1: The relative time improvement of L2Sep over the SCIP solver**

L2Sep accelerates state-of-the-art MILP solver Gurobi

**Table 2: The relative time improvement of L2Sep over Gurobi**

L2Sep recovers effective separators from literature

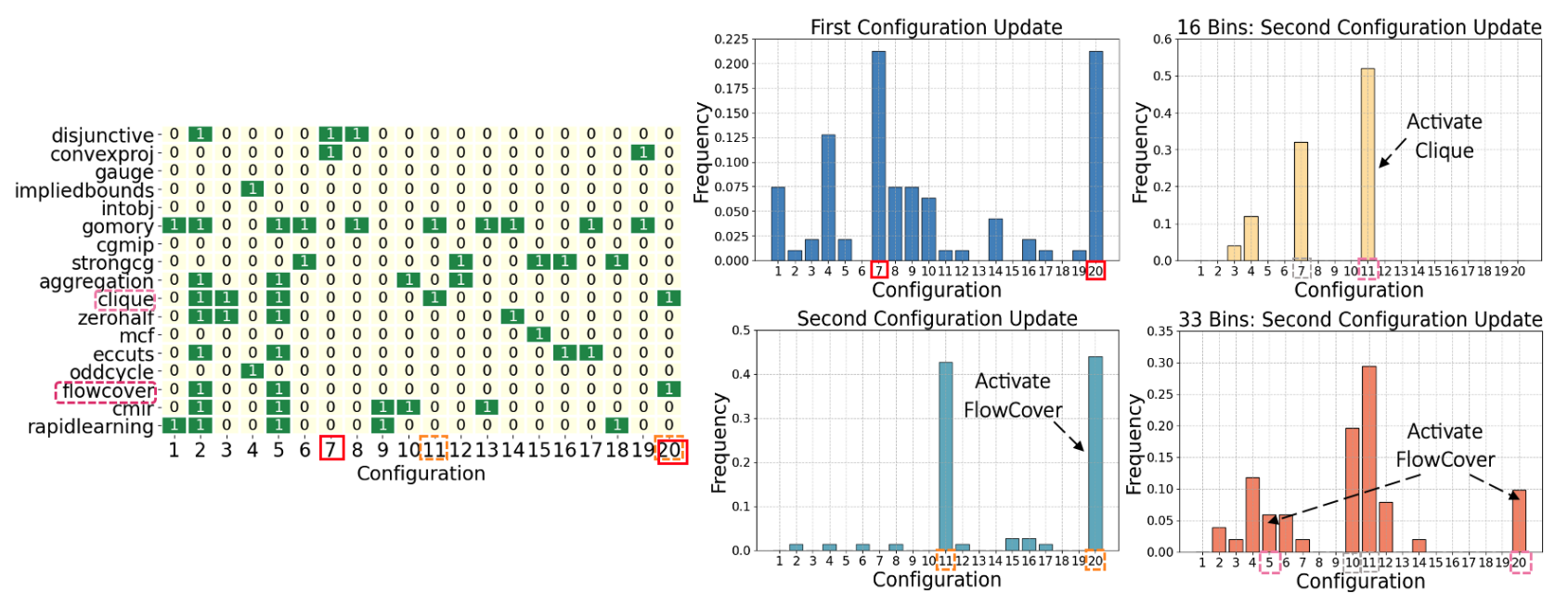
**Figure 4: Bin Packing Interpretation.**

(Left / Heatmap) Each row is a separator, and each column is a configuration in our restricted space. Green and yellow cells indicate activated and deactivated separators by each configuration, respectively.

(Middle / Histogram Left Column) The frequency of each configuration selected by our learned model at the 1st and 2nd config. update on the original test set with 66 bins. The config. indices in the heatmap and the histograms align.

(Right / Histogram Right Column) The frequency of each configuration selected at the 2nd config. update (the 1st update has similar results) when we gradually decrease the number of bins (bottom: 33 bins; top 16 bins). We observe the prevalence of FlowCover and Clique decreased and increased, respectively.

L2Sep is effective under an alternative objective: relative gap improvement

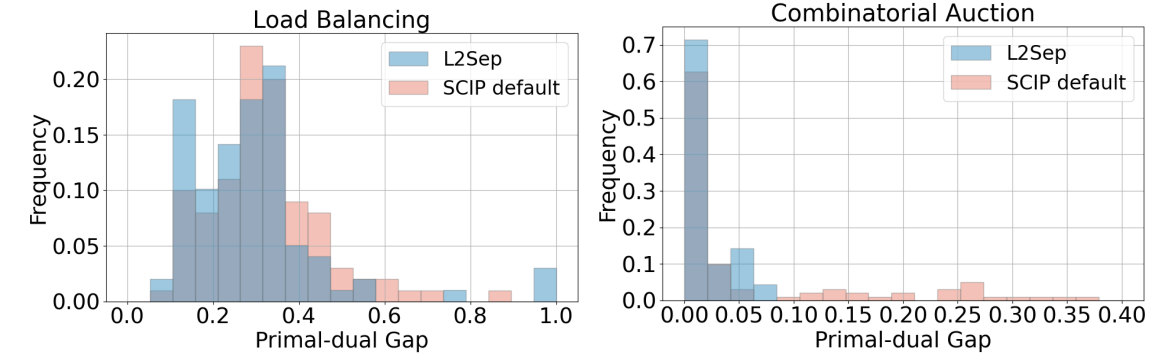
**Figure 5: Distributions of absolute primal-dual gaps of L2Sep and SCIP default on Load Balancing and Combinatorial Auction**

Acknowledgement

This work was supported by a gift from Mathworks, the National Science Foundation (NSF) CAREER award (#2239566), the MIT Amazon Science Hub, and MIT’s Research Support Committee. The authors acknowledge the MIT SuperCloud and Lincoln Laboratory Supercomputing Center for providing HPC resources that have contributed to the research results reported within this paper. The authors would like to thank Mark Velednitsky and Alexandre Jacquillat for insightful discussions regarding an interpretative analysis of the learned model.